[JS/Sorting] 퀵 정렬, 자바스크립트로 구현하기 (Quick Sort in JavaScript)

Quick Sort

퀵 정렬은 1960년에 찰스 앤터니 리처드 호어(C.A.R hoare)가 처음 제안한 방법으로 이후 많은 사람들이 수정 보완하여 완성된 정렬 알고리즘이다. 이 알고리즘은 처음 소개된 이후로 반세기가 넘었지만 현존하는 가장 빠른 정렬 알고리즘 중에 하나이다. 퀵 정렬은 in place 방법과 in place가 아닌 방법 2가지가 있는데 실제로 많이 쓰이는 방법은 메모리 사용량이 적은 in place 방법이다. 그러나 in place가 아닌 방법이 더 직관적으로 이해하기 쉬우므로 이 방법을 먼저 정리하고 그 다음 in place 방법을 정리하겠다.

 

Basic Quick Sort - Not In Place

퀵 정렬은 지난번 병합 정렬 포스팅에서 소개한 Divide and Conquer 전략을 사용한 알고리즘이다. 

즉, 정렬하는데 가장 간단한 배열은 바로 요소가 없거나 하나만 있는 배열이므로 모든 배열이 기본 배열이 될 때까지 큰 배열을 나눠야한다.

이 때 퀵 정렬에서는 요소 하나를 기준 원소인 pivot으로 설정한다. 그리고 기준 원소의 왼쪽에는 기준 원소보다 작은 값의 배열을 놓고 오른쪽에는 기준 원소보다 큰 값을 놓는다.

pivot 왼쪽에 놓여진 기준 원소보다 작은 배열에서 위와 같은 방법으로 다시 pivot을 설정하고 배열을 pivot을 기준으로 나눈다. 이 방법을 반복하면 결국 기본 단계인 원소가 하나만 있는 배열이 남는다.

 

Basic Quick Sort

 

그림으로 표현하면 위와 같다.

 

1. 기준 원소를 고른다. 여러 가지 방법이 있겠지만 위 그림에서는 배열의 첫 번째 요소를 기준 원소로 설정했다.
2. 배열을 기준 원소보다 작은 원소의 배열과 기준 원소보다 큰 원소의 배열, 이렇게 2개의 하위 배열로 분할한다.
3. 하위 배열에 대해 재귀적으로 퀵 정렬을 호출한다.

 

위 방법의 퀵 정렬은 in place 방법이 아니기 때문에 별도의 메모리 공간이 필요하므로 데이터의 양이 많으면 공간적인 낭비가 심해져 실제로는 잘 쓰이지 않는 방법이다. 그러나 위의 방법으로 퀵 정렬을 할 경우에 중복되는 데이터는 순차적으로 pivot에 넣으면 되기 때문에 정렬 전 중복 데이터의 순서가 바뀌지 않는 stable한 정렬을 구현할 수 있다.

 

 

function quickSort (array) {
  if (array.length < 2) {
    return array;
  }
  const pivot = [array[0]];
  const left = [];
  const right = [];

  for (let i = 1; i < array.length; i++) {
    if (array[i] < pivot) {
      left.push(array[i]);
    } else if (array[i] > pivot) {
      right.push(array[i]);
    } else {
      pivot.push(array[i]);
    }
  }
  console.log(`left: ${left}, pivot: ${pivot}, right: ${right}`);
  return quickSort(left).concat(pivot, quickSort(right));
}

const sorted = quickSort([5, 3, 7, 1, 9]);
console.log(sorted);

 

위의 방법으로 퀵 정렬을 구현하는 것은 매우 쉽다.

array의 길이가 1 이하이면 해당 배열을 그대로 return하고

원소의 0번째 요소를 pivot으로 잡는다.

left와 right 배열을 새로 만든 후,

0번째 요소 다음 요소부터 순회하며 pivot과 값을 비교하여

left 배열, right 배열에 데이터를 push한 후 

하위 배열에 대해 다시 재귀 호출을 하면서 세 배열을 합쳐준다.

 

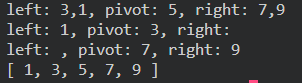
실행결과

 

 

In place Quick Sort

위의 방법은 이해하기에 훨씬 쉽고 구현도 간단하지만 메모리 공간의 낭비가 심하기 때문에 위 방법보다는 in place 방법이 훨씬 더 많이 사용된다.

 

 

In place Quick Sort

 

개념은 위의 그림과 같다.

 

정렬되지 않은 데이터에서 가운데 원소를 pivot으로 설정하고 가장 왼쪽 요소와 가장 오른쪽 요소가 시작점이다.

 

가장 왼쪽부터 값을 pivot값을 비교하여 pivot보다 큰 값이 나타날 때까지 칸을 오른쪽으로 이동한다.

가장 오른쪽부터 값을 pivot값을 비교하여 pivot보다 작은 값이 나타날 때까지 칸을 왼쪽으로 이동한다.

pivot보다 큰 왼쪽 값과 pivot보다 작은 오른쪽 값을 서로 교환한다.

 

왼쪽 인덱스가 오른쪽 인덱스보다 커지면 이동을 멈추고 그 자리에서 두 배열로 갈라서

각 배열에 위와 같은 방식으로 재귀 호출하여 정렬한다.

 

이 방법은 추가적인 공간을 필요로하지 않기 때문에 메모리 공간이 절약된다는 장점이 있으나, 왼쪽과 오른쪽 값을 교환하는 과정에서 중복값의 위치가 바뀔 수 있으므로 unstable한 정렬 방법이다.

 

 

function quickSort (array, left = 0, right = array.length - 1) {
  if (left >= right) {
    return;
  }
  const mid = Math.floor((left + right) / 2);
  const pivot = array[mid];
  const partition = divide(array, left, right, pivot);

  quickSort(array, left, partition - 1);
  quickSort(array, partition, right);

  function divide (array, left, right, pivot) {
    console.log(`array: ${array}, left: ${array[left]}, pivot: ${pivot}, right: ${array[right]}`)
    while (left <= right) {
      while (array[left] < pivot) {
        left++;
      }
      while (array[right] > pivot) {
        right--;
      }
      if (left <= right) {
        let swap = array[left];
        array[left] = array[right];
        array[right] = swap;
        left++;
        right--;
      }
    }
    return left;
  }

  return array;
}

퀵 정렬은 위와 같이 구현할 수 있다. 

먼저 배열의 왼쪽 인덱스와 오른쪽 인덱스의 기본값을 각각 0과 array.length - 1로 설정한다.

그리고 중간 pivot값을 구한다.

 

이제 divide라는 함수를 통해 왼쪽과 오른쪽 인덱스를 이동하며 값을 교환하고 partition으로 설정할 인덱스를 리턴받는다. 리턴받은 partition 인덱스를 기준으로 배열을 왼쪽 배열, 오른쪽 배열로 나눠서 다시 재귀 호출을 한다.

 

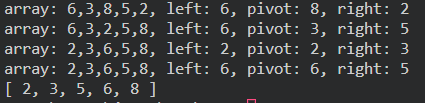
실행결과

 

Big O

• Worst Case: O(n^2)
• Best Case: O(nlog₂n)

퀵 정렬은 대개의 경우 매우 좋은 성능을 보여준다. 최선의 경우에는 스택의 크기가 O(log₂n)이고 각 스택마다 요소의 개수만큼 검색하므로 총 O(n)을 순회하기 때문에 결과적으로 시간 복잡도는 O(nlog₂n)이다.

그러나 최악의 경우에는 스택의 크기가 O(n)이 되고 O(n)번 순회하므로 O(n^2)이란 시간이 소요된다.

 

quickSort([1, 2, 3, 4, 5, 6, 7]);
quickSort([5, 8, 1, 3, 9, 4, 7]);

 

만약에 우리가 위의 코드처럼 두 번의 퀵 정렬을 수행한다고 해보자.

이 때 첫 번째 실행문에서 정렬할 배열은 이미 정렬이 완료된 배열이고 두 번째 실행문에서 정렬할 배열은 값이 뒤섞여있는 배열이다. 만약에 pivot값을 배열의 첫번째 원소로 지정한다고 했을 때 실행결과를 살펴보자.

 

 

실행결과

 

이미 정렬된 배열의 경우 7번의 재귀 호출을 한 끝에 정렬이 완료되었으나

뒤섞여있던 배열은 5번의 재귀 호출을 한 끝에 정렬이 완료되었다.

 

이처럼 이미 정렬된 배열을 첫번재 원소를 기준으로 퀵 정렬하는 경우가 바로 최악의 시나리오이다.

그러나 일반적인 경우에는 최선의 경우와 같은 실행 속도를 가지며 평균적으로 O(nlog₂n) 실행 시간을 가지는 매우 빠른 정렬 방법 중의 하나이며 분할 정복의 좋은 예이다.

 

 

 

---

참고자료:

• http://www.algolist.net/Algorithms/Sorting/Quicksort
• Hello Coding 그림으로 개념을 이해하는 알고리즘, 마야트먀 바르가바 지음, 한빛미디어
• 알고리즘 문제 풀이 전략, 조중필, 한현상, 이주호 공저, 한빛미디어