[JS/Sorting] 병합 정렬(Merge Sort)과 분할 정복 전략(Divide and Conquer) 개념에 대하여

Merge Sort

병합 정렬 혹은 합병 정렬이라고 불리는 Merge Sort는 데이터들을 잘게 쪼갠 다음에 하나로 합치는 과정에서 정렬하는 방법이다. 요즘은 데이터를 USB같은 장치로 저장하는 것이 일반적이었으나 아주 옛날에는 테이프를 이용해서 저장했다. 테이프 드라이브에 저장된 데이터를 정렬하는 일은 매우 어려운 일이었다. 왜냐면 테이프 드라이브는 항상 데이터를 처음부터 순차적으로 읽어야 한다는 특징이 있기 때문이다. 이러한 테이프 드라이브의 문제점 때문에 병합 정렬 알고리즘이 탄생하였다. 

 

 

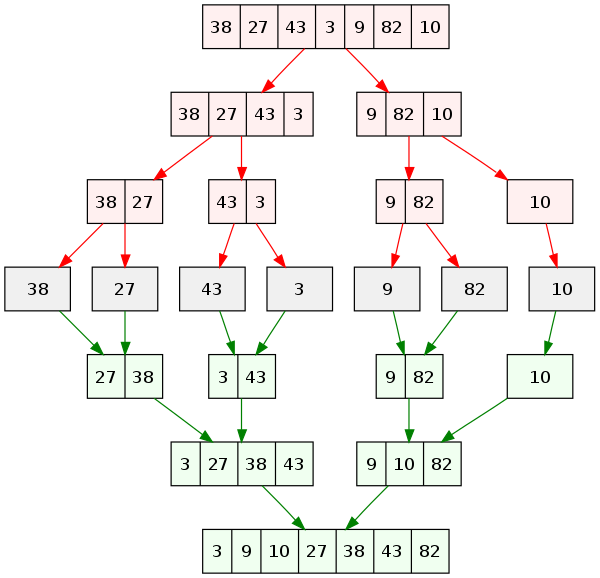
Merge Sort

 

병합 정렬은 위의 그림처럼 데이터를 절반씩 쪼개는 divide 작업을 먼저 하는데 이 작업은 데이터가 하나만 남을 때까지 반복한다. 그 후에 하나씩 쪼개진 데이터를 정렬을 하면서 다시 그룹화한다. 

이런 과정은 아래 gif로 첨부한 이미지를 보면 좀 더 이해하기 쉽다.

 

---

 

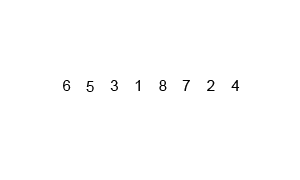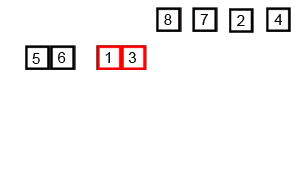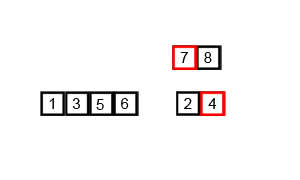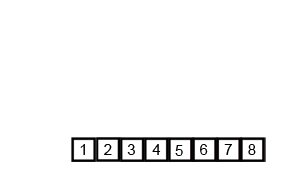
Divide and Conquer

Divide and Conquer, 즉 분할하여 정복한다는 이 기법은 알고리즘 문제를 해결하는 유명한 전략 중 하나이다. 예를 들어서 다음 문제를 살펴보자.

 

 

 

만약 우리가 이렇게 생긴 땅을 가지고 있고 이 땅을 정사각형 토지로 잘게 나누고 싶다고 생각해보자. 정사각형 토지는 가능한한 크게 하고 모든 정사각형 토지의 크기는 같아야한다. 이런 문제를 해결하기 위해 우리는 분할 정복 전략을 사용할 수 있다. 전략은 다음과 같다.

 

1. 기본 문제를 해결한다. 이 부분은 가능한 한 간단한 문제여야 한다.
2. 문제가 기본 단계가 될 때까지 나누거나 작게 만든다.

 

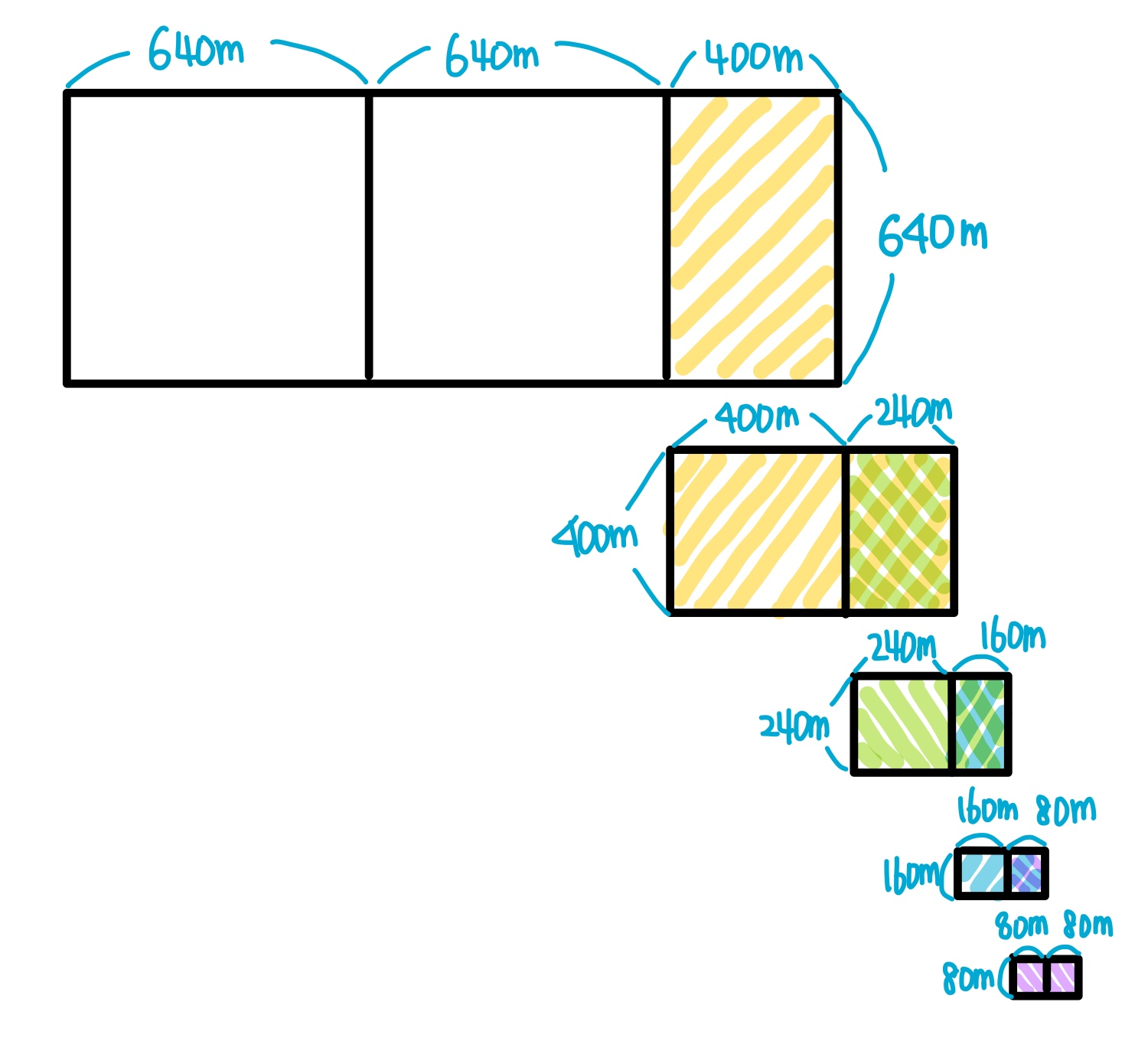
즉, 토지의 세로 길이로 정사각형 2개를 만든다. 그러면 두 개의 정사각형 토지와 아직 나누지 못한 토지로 나눠진다. 

그러면 아직 나누지 못한 남은 토지도 똑같은 방법으로 나눈다.

 

단계를 거칠 때마다 우리가 원래 풀던 1680m X 640m 토지 나누기 문제가 640m X 400m → 400m X 240m → ... 이런 식으로 점점 작아진다.

 

이 방법을 재귀적으로 풀다보면 결국 맨 마지막에는 80m 정사각형 토지 2개로 나눠진다.

즉, 1680m X 640m 크기의 땅을 나눌 수 있는 가장 큰 정사각형의 크기는 80m X 80m인 것이다.

 

분할 정복 전략은 다음과 같이 동작한다.

 

1. 가장 간단한 경우로 기본 단계를 찾는다.
2. 주어진 문제를 가능한한 작게 줄여서 기본 단계가 되게끔 만드는 법을 찾는다.

 

---

 

 

만약에 배열에 든 숫자의 합계를 구하는 문제가 있다고 해보자. 물론 반복문을 사용하면 아주 쉽게 구할 수 있지만 이 문제를 Divide and Conquer 전략을 사용하여 재귀 함수로 구한다면 어떻게 구할 수 있을까?

 

1. 먼저 기본 단계를 찾는다. 기본 단계는 원소의 개수가 0개이거나 1개인 배열을 받을 때이다. 
2. 재귀 호출을 할 때마다 호출 대상이 되는 배열의 크기를 줄인다. sum([1, 2, 3])은 1 + sum([2, 3])으로도 계산 가능하므로 sum 함수에 더 작은 배열을 넘겨 문제의 크기를 줄인다.

 

 

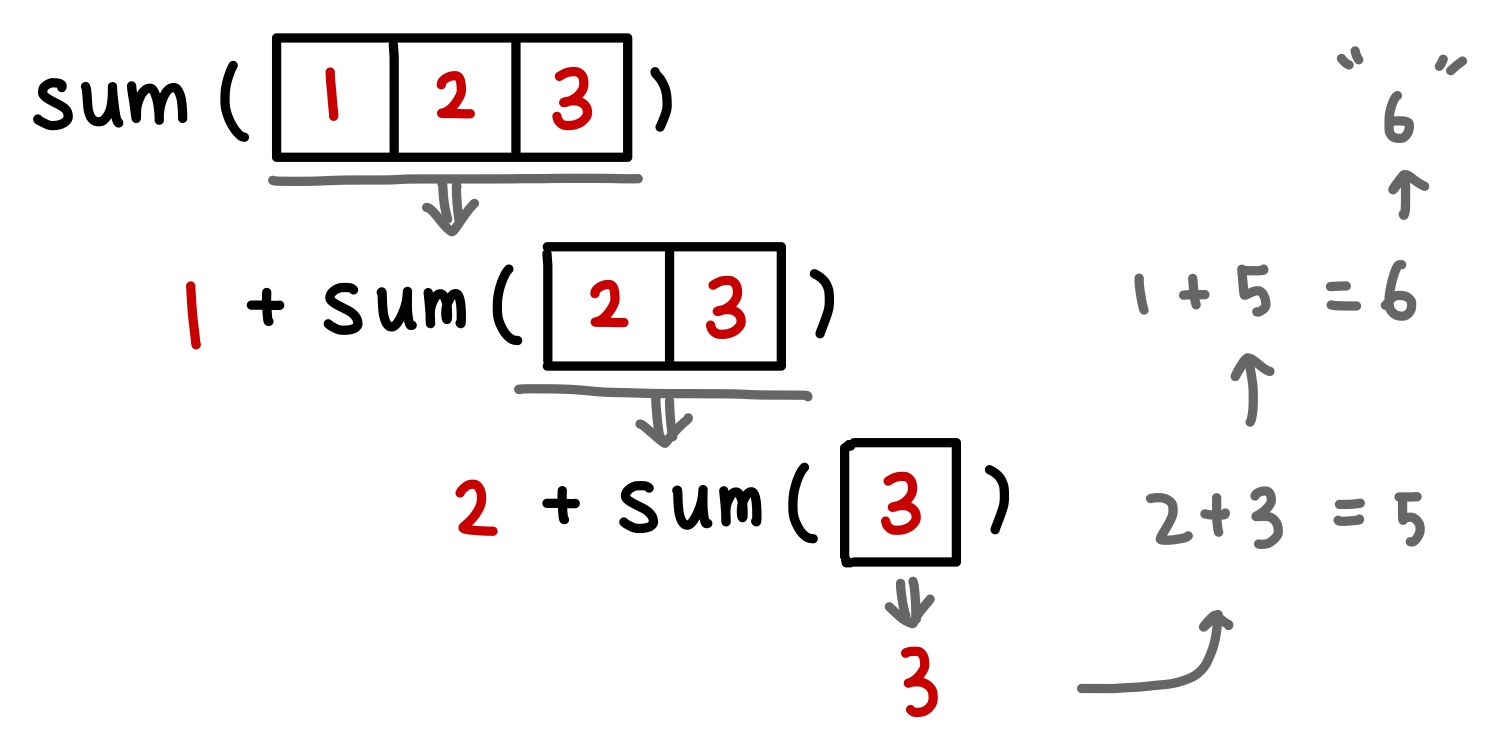
function sumNum (arr) {
  if (arr.length === 0) {
    return 0;
  }
  if (arr.length === 1) {
    return arr[0];
  }
  return arr[0] + sumNum(arr.slice(1));
}
sumNum([1, 2, 3, 4, 5]);  // 15

코드로 표현해보면 이런 식이다.

 

 

---

 

다시 병합 정렬로 넘어가보자. 병합 정렬 역시 Divide and Conquer 전략을 사용한 알고리즘으로 문제의 크기를 줄여서 작은 것부터 정렬을 해나가며 결과적으로 모든 데이터를 정렬하는 방법이다. 

 

Big O

• Worst Case: O(nlog₂n)
• Best Case: O(nlog₂n)

병합 정렬은 데이터를 분할하는 단계와 다시 병합하는 단계로 나눌 수 있는데, 분할하는 단계는 시간복잡도에 포함되지 않는다.

 

데이터를 분할한 후 병합하는 단계에서 재귀 호출의 길이는 log₂n이다. 왜냐하면 1/2씩 쪼개진 배열을 합치기 때문이다. 그리고 그 각각의 단계에서 데이터의 개수만큼 크기를 비교하는 연산이 필요하기 때문에 최대 n번의 비교 연산을 하게 된다. 그러므로 병합 정렬의 시간 복잡도는 O(nlog₂n)이며 이는 최선의 경우이든 최악의 경우이든 동일하게 적용된다.

 

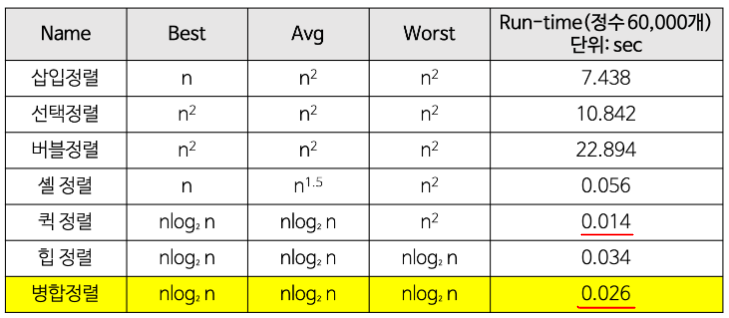
병합 정렬은 최선의 경우와 최악의 경우가 모두 O(nlog₂n)의 시간을 가지기 때문에 최악의 경우에 O(n^2)의 시간을 가지는 퀵 정렬보다 빠른 정렬이라고 생각하기 쉽다. 그러나 항상 그런 것은 아니다. 그 이유는 퀵 정렬이 병합 정렬보다 더 작은 상수 시간을 가지기 때문이다. 

 

예를 들어서 어떤 배열을 단순히 콘솔 창에 하나씩 출력하는 함수는 O(n)의 시간이 소요된다. 그런데 만약 setTimeout을 사용하여 콘솔 창에 출력하기 전 1초의 딜레이를 준다고 생각해보자. 이 경우 콘솔 창에 데이터를 출력할 때마다 1초를 더 기다려야하므로 실제 함수 실행 시간은 느려진다. 그러나 빅오 표기법에서는 이런 상수들을 보통 무시하기 때문에 두 함수 모두 O(n)이라고 표기한다.

 

퀵 정렬과 병합 정렬의 경우에도 두 정렬의 소요시간은 최선의 경우에 모두 O(nlog₂n)이라고 표현되지만 퀵 정렬이 병합 정렬보다 작은 상수값을 가지므로 최악의 경우가 아닌 경우엔 퀵 정렬이 병합 정렬보다 좀 더 빠르다.

 

 

 

장점

병합 정렬은 최선의 경우에도, 최악의 경우에도 O(nlog₂n)의 시간이 소요되기 때문에 데이터 분포에 영향을 덜 받는다. 항상 동일한 시간이 소요되므로 어떤 경우에도 좋은 성능을 보장받을 수 있다.

 

 

단점

병합 정렬은 in place 알고리즘이 아니기 때문에 별도의 메모리 공간이 필요하다. 만약에 정렬할 데이터의 양이 많은 경우에는 그만큼 이동 횟수가 많아지므로 시간적인 낭비도 많아지게 된다.

 

 

Stable

병합 정렬은 중복된 데이터의 순서가 바뀌지 않는 stable한 정렬이다.

 

 

function mergeSort (array) {
  if (array.length < 2) {
    return array;
  }
  const mid = Math.floor(array.length / 2);

  const left = array.slice(0, mid);
  const right = array.slice(mid);

  return merge(mergeSort(left), mergeSort(right));

  function merge (left, right) {
    const resultArray = [];
    let leftIndex = 0;
    let rightIndex = 0;

    while (leftIndex < left.length && rightIndex < right.length) {
      if (left[leftIndex] < right[rightIndex]) {
        resultArray.push(left[leftIndex]);
        leftIndex++;
      } else {
        resultArray.push(right[rightIndex]);
        rightIndex++;
      }
    }

    return resultArray.concat(left.slice(leftIndex), right.slice(rightIndex));
  }
}
console.log(mergeSort([5, 4, 3, 2, 1]));

 

자바스크립트 코드로 구현한 Merge Sort이다.

Merge Sort는 배열을 쪼개는 단계와 병합하는 단계로 나눠진다.

먼저 array의 길이가 2보다 작으면 분할이 끝난 것이므로 array를 그대로 return한다.

만약 2보다 크다면 반으로 나눈다.

 

left와 right으로 나눠진 배열은 각각 merge라는 함수를 호출하여 병합한다.

merge함수는 최종으로 합쳐진 배열을 담을 resultArray라는 배열을 준비하고

두 배열의 앞자리 숫자부터 비교하여 배열에 담는다.

while문을 빠져나오면 두 배열 중 숫자가 작은 한 쪽 배열의 요소가 resultArray에 담기기 때문에

resultArray에 left와 right 배열을 다시 합치고 리턴한다.

 

 

실행결과

 

---

참고자료:

• https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/sorting/merge-sort
• https://gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
• https://ko.wikipedia.org/wiki/%ED%95%A9%EB%B3%91_%EC%A0%95%EB%A0%AC
• Hello Coding 그림으로 개념을 이해하는 알고리즘, 마야트먀 바르가바 지음, 한빛미디어
• 알고리즘 문제 풀이 전략, 조중필, 한현상, 이주호 공저, 한빛미디어