[자료 구조] Data Structure - (1) Stack / Queue / Linked List

자료 구조는 코딩과는 별로 상관없는 것처럼 보일 수도 있겠지만

사실 프로그래밍에 있어서 매우 중요한 부분을 차지한다.

 

내가 어떠한 프로그램을 구현할 때, 혹은 어떤 알고리즘 문제를 해결하거나 새로운 로직을 만들어야할 때

데이터들을 어떤 구조로 저장하느냐에 따라서 프로그램의 효율성이나 성능 면에서 차이가 날 수 있기 때문이다.

따라서 오늘은 자료 구조 중에서 가장 기본적인 3가지를 간단하게 정리해보려고 한다.

 

 

Stack (스택)

Stack은 자료를 한 줄로 블록을 쌓듯이 추가하는 형태의 자료 구조이다.

Stack의 맨 위에 자료를 추가하는 것을 우리는 push라고 하고

반대로 맨 위의 자료를 하나씩 제거하는 것을 우리는 pop이라고 한다.

 

push

 

pop

 

위 그림처럼 스택은 어느 한 곳에 블록처럼 자료가 쌓이기 때문에

스택에서 어떤 자료를 제거할 때는 가장 마지막에 들어간 자료가 가장 먼저 제거된다.

(LIFO: Last-In First-Out)

 

 

 

Big O (빅오: 시간 복잡도)

 

우리가 만약 스택이라는 자료 구조를 선택해서 자료를 삽입하고 삭제하고 검색하는 일련의 과정을 거친다고 생각해보자. 이 때 우리가 자료를 삽입, 삭제, 검색하는 일련의 행동들이 정확히 컴퓨터 상에서 몇 초 동안 수행되는지 정확히 알 수는 없다. 그렇기 때문에 우리는 몇 초 동안에 수행되는지가 아니라 어떤 연산을 하는데 몇 차례의 과정을 거치는지 횟수를 세는 방법으로 대략적인 소요 시간과 효율성을 측정할 수 있다. 이렇게 수행되는 연산의 수를 가지고 계산할 때에는 알고리즘에서 중요하지 않는 값들은 최대한 무시한다.

이 때 연산 과정을 간편하게 표기해서 쓸 수 있는 수학적인 표기법을 Big O(빅오)라고 부른다.

 

이 빅오 표기법으로 스택의 시간 복잡도를 표기해보면 다음과 같다.

 

Insertion	O(1)
Deletion	O(1)
Search	O(n)

 

O(1)이라는 표현에서 1은 constant 즉, 상수 시간을 말한다. 우리가 스택에 어떤 자료를 추가할 때를 생각해보자. 스택에 자료를 추가할 때는 항상 스택의 맨 위에 자료를 push하기만 하면 된다. 즉, 자료의 개수가 몇 개인지와 같은 다른 어떤 사항도 고려할 필요 없이 그냥 새로운 자료를 기존의 자료 맨 위에 올리기만 하면 된다는 뜻이다. 그러므로 한 번의 operation으로 자료의 삽입이 수행되므로 O(1)이라고 표기할 수 있다. O(1)이라는 것은 단 한 번의 연산이 된다는 뜻은 아니다. 어떤 작업을 수행할 때마다 항상 동일한 작업만을 수행한다면 그 작업들을 뭉뚱그려서 O(1)이라고 표현할 수 있다. 그러므로 O(1)은 한 번의 연산을 수행한다는 뜻이 아니라 매 번 동일한 작업을 수행한다는 뜻이다.

 

자료를 삭제할 때도 마찬가지이다. 자료의 개수가 몇 개이던지 그냥 맨 위에 있는 자료를 pop하면 되므로 자료의 삭제 또한 O(1)으로 표기할 수 있다.

 

그렇다면 자료의 검색은 어떨까? 만약에 스택에 5개의 블록이 쌓여있다면 우리는 맨 위의 블록에서부터 맨 마지막 블록까지 순차적으로 검색하여 자료를 찾아야할 것이다. 운이 좋게 첫 번째 블록이 우리가 찾는 블록이었다면 한 번의 검색으로 답을 찾을 수 있겠지만 만약에 맨 마지막 블록이 우리가 찾는 블록이라면 우리는 맨 마지막 블록이 나올 때까지 5번의 검색 과정을 거쳐야할 것이다. 그러므로 스택의 검색 횟수는 가장 최악의 경우인 O(n)으로 표기할 수 있다.

 

 

 

Real Life Use Cases

 

• 호출 스택(Call Stack): 예를 들어서 자바스크립트에서 모든 함수 호출은 스택 자료 구조로 이루어져있다. 특히 재귀함수를 사용할 때 중요하게 다뤄진다. (https://im-developer.tistory.com/102?category=831368)
• Undo/Redo Mechanism: 만약에 우리가 포토샵같은 프로그램을 켜서 사진 작업을 한다고 해보자. 사진을 밝게 조절하기도 하고 색깔 톤을 조절하기도 하고 필터를 사용할 수도 있다. 작업을 하다가 결과가 마음에 안들면 언제든지 Ctrl+Alt+Z를 눌러서 방금전의 작업들을 뒤에서부터 순차적으로 취소할 수 있다. 이러한 매커니즘도 스택과 같은 자료구조라고 할 수 있다. 우리가 실행한 보정 작업들이 순차적으로 스택 구조로 저장되고 취소 단축키를 누를 때마다 맨 위의 자료들이 삭제되기 때문이다.

 

아래 링크는 스택 자료 구조를 활용하여 해결한 알고리즘 문제이다.

 

https://im-developer.tistory.com/78?category=831474

[알고리즘/자바스크립트] 괄호 짝 찾기 (Valid Braces)

 

 

---

 

Queue (큐)

자료의 한 쪽 끝에서 삽입과 삭제가 같이 일어나는 스택과는 달리

Queue는 자료의 한 쪽 끝에서 자료가 삽입되고

그 반대쪽 끝에서 자료가 삭제되는 구조이다.

자료의 추가는 Enqueue, 삭제는 Dequeue라고 부른다.

 

Enqueue

 

Dequeue

 

스택과는 다르게 먼저 들어간 요소가 가장 먼저 빠져나온다.

이는 마치 매표소나 은행 창구에 줄을 선 것과 동일한 구조이다.

가장 먼저 와서 기다린 사람이 가장 먼저 서비스를 받고 줄에서 빠져나온다.

(FIFO: First-In First-Out)

 

 

 

Big O (빅오)

 

Insertion	O(1)
Deletion	O(1)
Search	O(n)

 

큐 역시 스택과 동일한 시간 복잡도를 가진다. 즉, 자료가 삽입될 때는 자료의 맨 뒤에 자료가 삽입되는 연산만 수행되므로 O(1)로 표기할 수 있다. 자료의 삭제 또한 맨 앞의 자료가 삭제되는 동일한 연산이 수행되므로 O(1)로 표기된다.

자료를 검색할 때는 맨 앞의 요소부터 맨 마지막 요소까지 차례대로 검색해야 하기 때문에 시간 복잡도는 O(n)이다.

 

만약에 자료가 100개 존재할 때, 30번 째 요소를 삭제한다면 그 때의 시간 복잡도는 어떻게 될까? 100개 중에 30번째 요소를 찾기 위해 자료를 검색하는 데 O(n)만큼이 소요되고, 그 후 검색한 해당 요소를 삭제하는 연산은 O(1)만큼 소요된다. 따라서 어떤 위치의 요소를 삭제하던지 항상 O(1)의 시간 복잡도가 소요된다.

 

 

 

Real Life Use Cases

 

• Line of people standing for food: Queue는 급식 배식을 받기 위해 차례대로 줄을 서 있는 구조이다.
• Callback queue: 지난번에 이벤트 루프에 대해서 정리할 때 설명한 적이 있다. 자바스크립트는 함수 호출을 스택 구조로 저장하는데, 우리가 만약에 setTimeout이나 Ajax, 혹은 돔 이벤트 함수들을 실행하면 브라우저는 해당 동작을 Web APIs로 보낸 후 요청한 시간이 되었을 때, 혹은 이벤트가 trigger되었을 때 Callback Queue에 순차적으로 동작을 적재하고 맨 앞에 있는 콜백부터 차례대로 호출 스택으로 보내 함수를 실행시킨다. (https://im-developer.tistory.com/113?category=831368)

 

---

 

Linked List (연결 리스트)

Linked List is made of a bunch of nodes that point to the next one in the list.

Linked List는 여러 노드들이 아래의 그림과 같은 구조로 연결되어있는 구조이다.

연결 리스트의 맨 앞을 head라고 하고 맨 마지막을 tail이라고 한다.

이 노드들은 다음에 올 노드의 정보를 가지고 있다.

 

Linked List

 

만약에 우리가 생일을 맞은 가족이나 애인을 위해 특별한 이벤트를 준비했다고 생각해보자.

 

방문 앞에 "거실의 2번째 칸 서랍으로 가시오"라는 메모를 붙여두었다.

그리고 2번째 칸 서랍에는 "주방 찬장 3번째 칸으로 가시오"라고 붙였다.

그리고 주방 천장의 3번째 칸에 작은 선물을 넣어두었다고 생각해보자.

 

이 때 우리는 선물을 찾기 위해서는 순차적으로 쪽지를 찾아다니며

쪽지에 써있는 다음 장소의 정보를 읽어야만 한다.

바로 이러한 구조가 연결 리스트이다.

 

 

 

Big O (빅오)

 

Insertion	O(1)
Deletion	O(1)
Search	O(n)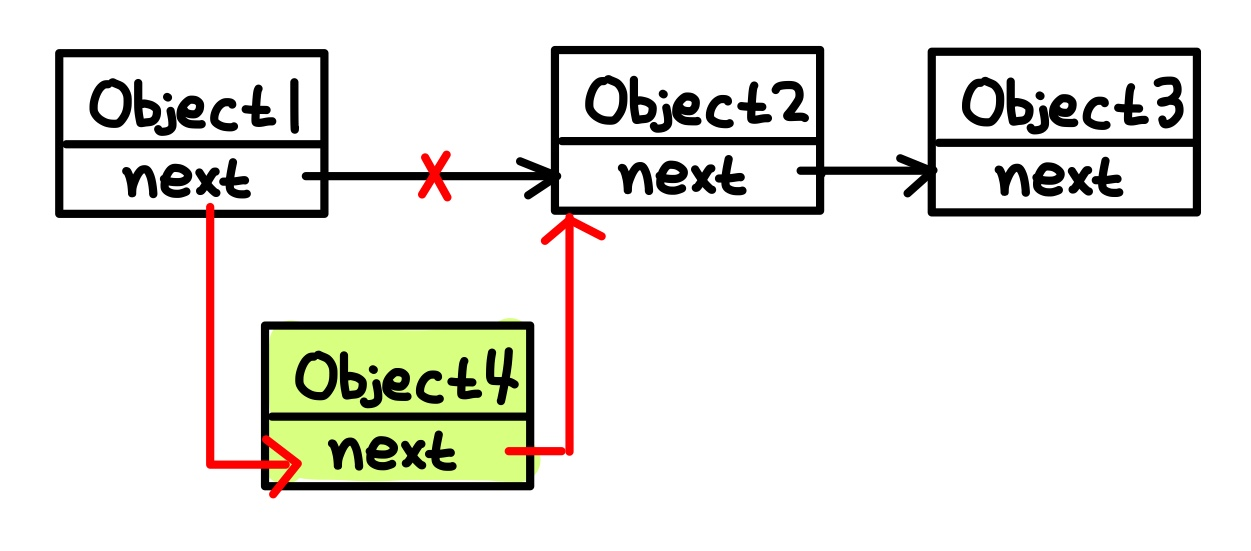

 

Insertion

 

만약 연결 리스트에 자료를 삽입하려고 한다면 우리는 위 그림과 같이

자료를 추가할 장소로 가서 기존의 링크를 끊은 다음

추가할 위치의 이 전 요소의 꼬리와 삽입할 자료의 꼬리를 연결한다.

그리고 추가할 요소의 꼬리와 다음 요소의 꼬리를 연결해주면 된다.

 

이 때에도 오직 앞 요소와 다음 요소와 연결시켜주는 operation만 수행되므로 시간 복잡도는 O(1)이다.

 

 

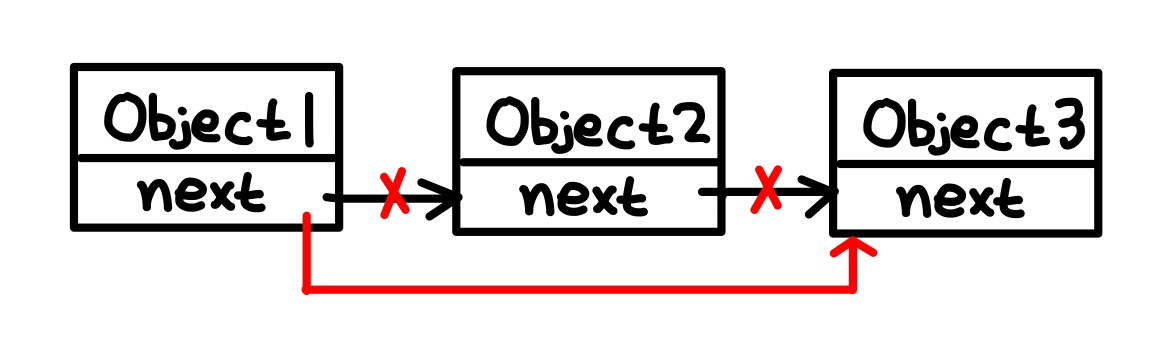
Deletion

 

만약에 연결 리스트에 특정 자료를 삭제하려고 한다면 위 그림처럼

삭제하고자 하는 요소의 이 전 요소의 꼬리를 다음 요소와 연결시켜주면 된다.

 

삭제하고자 하는 요소의 이 전 요소와 다음 요소를 연결시켜주는 operation이 수행되므로 시간 복잡도는 O(1)이다.

 

 

만약 연결 리스트에서 자료를 검색하고 싶다면 맨 앞의 head에서부터 시작해야한다.

왜냐면 연결 리스트의 각 노드들은 다음 요소들의 정보를 가지고 있기 때문이다.

그러므로 맨 앞의 리스트에서부터 그 다음의 노드들로 순차적으로 검색해야 한다.

이 때의 시간 복잡도는 O(n)으로 표기할 수 있다.

 

 

 

Real Life Use Cases

 

• The history section of web browers: 웹 브라우저에서 여러 사이트들을 실행하고 난 후 history는 연결 리스트와 같은 구조로 저장된다. 내가 어떤 사이트들에서 다른 사이트로 넘어갈 때, 이전 사이트의 정보를 가지고 넘어가기 때문이다. 따라서 우리가 브라우저에서 이전 버튼, 혹은 다음 버튼을 누르면 이 전에, 혹은 다음에 열람했던 사이트들로 이동할 수 있다.
• Line of people standing for food: 급식을 배식받기 위한 줄이 연결 리스트의 구조를 띌 수도 있다.

 

---

 

번외로 수업시간에 구현해본 Stack과

두 개의 Stack을 이용하여 구현한 Queue이다.

 

var Stack = function () {
  this.storage = [];
  // add an item to the top of the stack
  this.push = function (value) {
    this.storage.push(value);
  };

  // remove an item from the top of the stack
  this.pop = function () {
    if (this.size() < 1) {
      return;
    }

    return this.storage.pop();
  };

  // return the number of items in the stack
  this.size = function () {
    return this.storage.length;
  };

  return this;
};

 

var Queue = function () {
  var inbox = new Stack();
  var outbox = new Stack();

  // called to add an item to the `queue`
  this.enqueue = function (value) {
    while (outbox.size()) {
      inbox.push(outbox.pop());
    }

    inbox.push(value);
  };

  // called to remove an item from the `queue`
  this.dequeue = function () {
    while (inbox.size()) {
      outbox.push(inbox.pop());
    }

    return outbox.pop();
  };

  // should return the number of items in the queue
  this.size = function () {
    while (outbox.size()) {
      inbox.push(outbox.pop());
    }

    return inbox.size();
  };
};