[자료 구조] Data Structure - (3) Tree / Binary Search Tree

Tree

트리(Tree)는 이름 그대로 나무를 거꾸로 뒤집어 놓은듯한 형태이다. 자료구조가 하나의 뿌리에서 뻗어나가는 형상을 하고 있다. 트리 구조는 우리 일상에서 흔히 볼 수 있는 계층적인 구조(Hierarchical Structure)를 컴퓨터에서 표현한 구조이다. 한 가족의 족보나 회사의 조직도 등이 바로 트리 구조이다. 족보같은 경우 조상으로부터 자식, 자식의 자식, 자식의 자식의 자식 형태로 이루어져있기 때문이다. 

컴퓨터의 파일 시스템이나 웹 페이지의 DOM 구조도 트리 구조이다.

 

 

 

 

트리 구조는 대개 위 그림과 같은 구조이다. 

 

트리의 각 요소들은 Node라고 부르고 가장 상위의 노드를 Root Node라고 부른다. 반대로 최하위 노드는 Leaf Node 혹은 Terminal Node라고 한다. Leaf Node는 자식 노드가 없는 트리 구조의 가장 하단에 있는 노드들을 말한다.

 

한 노드에 연결된 서브 트리의 개수를 차수라고 한다. 예를 들어서 B 노드의 차수는 2개이다. 만약에 한 트리 내의 차수가 모두 2개 이하라면 그 트리를 이진 트리(Binary Tree)라고 부른다.

 

현재 노드에 연결되어있는 상위 노드는 Parent Node이고 그 하위의 자식 노드는 Child Node이다. 같은 부모 노드를 갖는 노드는 형제 노드, 즉 Sibling Node이다. 이렇게 트리 구조의 용어는 정말로 가계도와 비슷하다.

 

Level은 루트 노드부터 해당 노드까지 경로를 찾는 데 방문한 총 노드의 수를 말한다. 트리의 최대 레벨 수는 트리의 height(높이) 혹은 depth(깊이)라고 한다. 위 그림의 트리 구조는 Level 1부터 Level 3까지 있고 트리의 높이는 3이다.

 

 

 

---

 

 

Binary Search Tree

트리는 종류가 매우 많지만 그 중에서도 가장 유명한 구조 중 하나다 Binary Search Tree(이진 탐색 트리)이다.

Binary Search Tree는 이진 트리이기때문에 모든 노드의 차수는 2개 이하여야만 한다.

그리고 모든 왼쪽 자식 노드는 부모의 값보다 작은 값을 가져야하고 

모든 오른쪽 자식 노드는 부모의 값보다 큰 값을 가져야한다는 특징이 있다.

 

Tree structure in which a node can have zero, one, or two subtrees.
Every node in the left has a smaller value than its parent node.
Every node in the right has a larger value than its parent node.

 

즉, 6, 2, 9, 5, 8, 3, 1이란 데이터를 이진 탐색 트리로 만들면 위의 그림처럼 된다.

가장 먼저 들어간 6이 Root Node가 된다.

2는 6보다 작기 때문에 6의 왼쪽 자식 노드가 된다.

9는 6보다 크기 때문에 6의 오른쪽 자식 노드가 된다.

5는 6보다 작고 2보다 크기 때문에 2의 오른쪽 자식 노드가 된다.

8은 6보다 크고 9보다 작기 때문에 9의 왼쪽 자식 노드가 된다.

...

이런 규칙으로 이루어져있기 때문에 이진 탐색 트리는 평균적으로 이진 탐색과 똑같이 빠른 시간 복잡도를 가진다.

 

Big O - average

• Insertion: O(log n)
• Deletion: O(log n)
• Search: O(log n)

 

만약 로그 시간이 이해가 안간다면 아래 링크를 참조해보자.

 

https://hackernoon.com/what-does-the-time-complexity-o-log-n-actually-mean-45f94bb5bfbf

What does the time complexity O(log n) actually mean? - By

 

Big O - worst case

• Insertion: O(n)
• Deletion: O(n)
• Search: O(n)

이진 탐색 트리는 대개의 경우 빠른 속도를 자랑하지만 몇 가지 단점이 있는데, 하나는 데이터를 임의 접근(random access)할 수 없다는 것이다. 예를 들어서 이 트리의 6번째 원소를 찾고싶다고 말 할 수 없다.

또한 트리가 균형이 맞지 않는 최악의 경우에는 데이터의 삽입과 삭제, 검색이 모두 O(n)만큼 소요된다. 이진 탐색 트리의 성능이 떨어지는 경우는 다음 그림과 같은 경우이다.

 

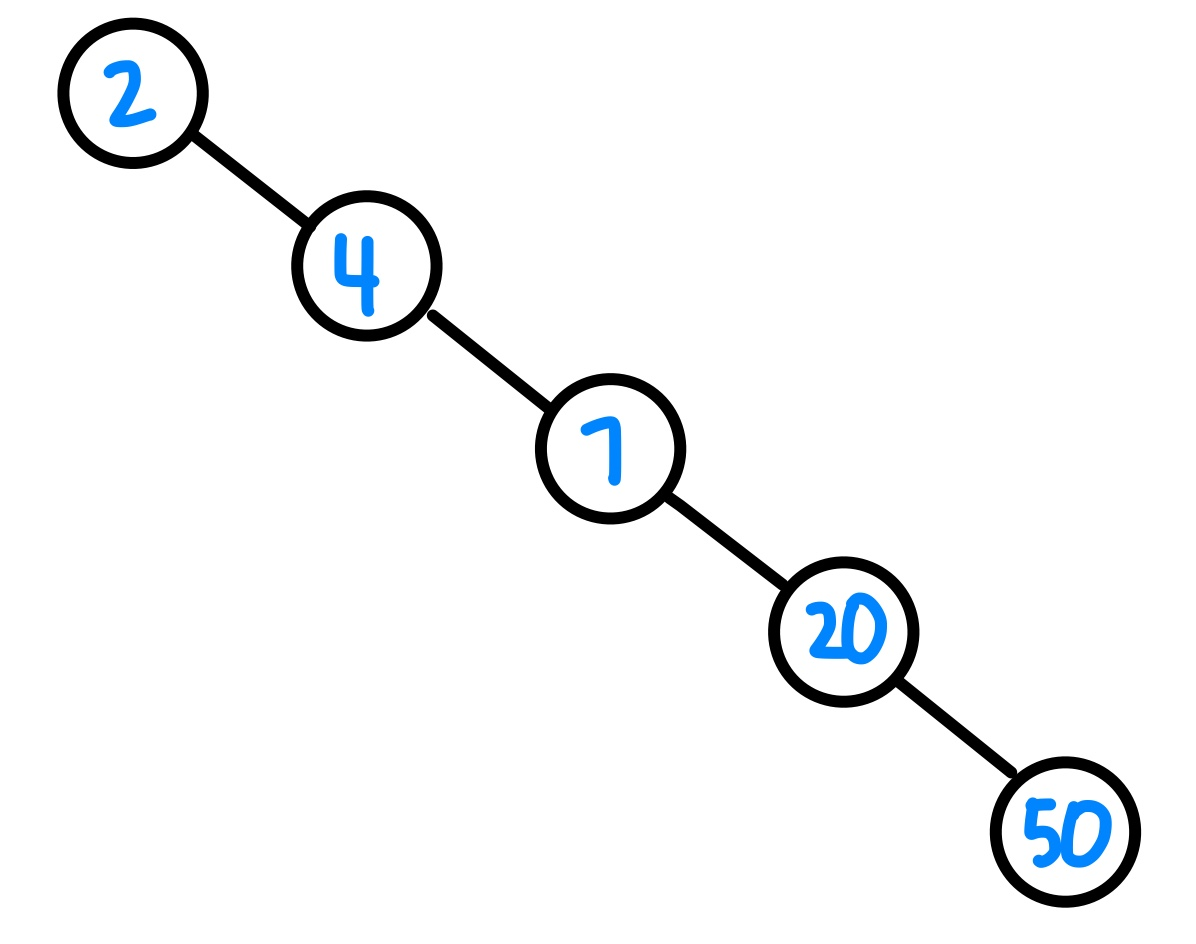
이렇게 데이터가 한쪽으로 치우쳐있으면 연결 리스트와 별 차이가 없는 구조가 되어 이진 트리의 장점이 사라진다. 이러한 이진 탐색 트리의 단점을 해결하기 위해 AVL 트리, 레드-블랙 트리, 2-3 트리 등 여러 가지 트리 구조가 존재한다.